3강은 오진석님께서 리뷰해주셨습니다. 3강에서는 네트워크의 Subgraph 에 초점을 둬서 Motif 라는 개념과 Graphlet 이라는 개념에 초점을 둡니다. 이 두가지만 정확하게 알고 넘어가도 80%는 성공입니다.
목차
1. Motifs
2. Graphlets : Node feature vectors
3. Finding Motifs and Graphlets
4. Structural Roles in Networks
5. Discovering Structural Roles in Networks
- Graph 에는 Subnetworks (Subgraph, building blocks of networks) 라는 개념이 있습니다.
- 이 개념들로 네트워크를 characterize 하고 discriminate(식별) 할 수 있습니다.
- 따라서 네트워크에 나타나는 비동형의 부분 그래프(non-isomorphoic)를 찾고 유의성(significance, 중요도)을 구합니다.


-> 3개에 노드에 대해서 edge 스타일에 따라 13개의 비동형 subgraph가 나올 수 있습니다. 이 각 subgraph에 대해서 중요도를 계산 후에 plot을 그려보면 오른쪽과 같은데, 이 때 0을 기준으로 양수인 것을 over-representation / 음수인 것을 under-representation 이라고 합니다. 도메인 별로 비슷한 양상을 띄는 것을 볼 수 있습니다. 맨 마지막 plot은 각 나라 언어에 대한 것인데 양상이 비슷합니다.
Subgraph에 속하는 motif 와 graphlet을 정의하고 찾아본 후에, 네트워크의 structural roles 에 대해 알아보겠습니다. structural roles를 찾는 방법도 간단하게 배웁니다.
1. Motifs
Network motifs : 'recurring, significant patterns of interconnections' 재귀적이고 유의한 연결 패턴입니다.
(motif는 음악의 주요 선율이라는 뜻도 있습니다. 연관지어서 이해하면 도움이 됩니다. )
motif를 정의하는 3가지 요소는 pattern, recurring, significant 입니다.
- Pattern : 작은 subgraph
- Recurring : high frequency, 여러번 발생
- Significant : 예상보다 더 많이 발생 (랜덤그래프가 예상된 값)
motif는 네트워크 작동의 이해를 돕고, 주어진 상황에서 네트워크의 작동과 대응을 예측할 수 있도록 도와줍니다.

Significance of a Motif
subgraph는 random graph model 로 생성한 네트워크보다 실제 네트워크(real world)에서 더 많이 일어납니다. 이를 이용해서 significance를 계산합니다.

각 노드에 대한 Z-score 의 식과, normalized Z-scores는 위와 같습니다. 보통 네트워크가 커질 수록 Z-score 가 커지기 때문에 비교를 위해서 normalize를 해줍니다.
Configure Model
real network 와 비교할 random graph가 필요하기 때문에, 차수가 주어질 때 랜덤그래프를 생성하는 방법으로 두가지를 소개합니다.
Spoke

- 먼저 spoke 가 있는 노드들을 준비합니다. (방향성 있는 spoke도 가능)
- 노드를 하나의 파티션으로 생각하고, spoke 끼리 연결을 합니다.
- 두번째 그림처럼 연결된 노드쌍(pair) 들을 그래프로 만들면 랜덤 그래프를 얻을 수있습니다.
- 이 방법은 굉장히 빠르고 효율적이지만, Double Edge나 Self-loops 는 고려하지 못해서 기존의 주어진 degree를 유지하지 못하는 단점이 있습니다. (nodeB의 경우)
Switching

- Switching은 edge들의 쌍을 선택해서 랜덤으로 exchange 하는 방법입니다.
- 왼쪽 그림에서는 A->B, C->D ---------> A->D, C->B 로 switching 되었습니다.
- Spoke 보다 expensive한 방법이지만 degree sequence를 지킬 수 있게 됩니다. 하지만 rewiring과정이 매우 느립니다.
- 보통 Q x E 번의 switching 을 해줍니다. (보통 Q =100)
real graph의 크기에 따라 달라지긴 하지만, 일반적으로 10,000개 ~ 100,000개의 랜덤그래프를 생성합니다. real graph와 동일한 갯수의 node, edge, degree distribution을 가지도록 configure model을 만든 후에는 real graph와 비교해서 significance를 구합니다. 가장 높은 significance (hige Z-score)를 가지는 subgraph를 해당 그래프를 대표하는 motif라고 볼 수 있습니다.
추가적으로 Motif 는 Concept에 따라서 다양합니다.

2. Graphlets : Node feature vectors
Graphlet: Connected non-isomorphic subgraph, 노드 주변의 노드는 어떻게 생겼을까? 를 graphlet 개념으로 포착합니다.
graphlet 개념을 사용한다면 주어진 node를 특징화 할 수 있습니다. 주어진 node를 바탕으로 network 구조를 설명할 수 있게 됩니다. -> node에 대한 node-level subgraph metric
Automorphism Orbits

직역하면 자기동형사상 입니다. 대칭적인 그래프를 나타낸다고 합니다.
Graphlet Degree Vector (GDV)
각 orbit position에서 node의 빈도에 대한 벡터를 의미합니다. (특정 orbit에서 노드에 인접한 graphlet의 갯수 -> vector)
그림을 보는 것이 이해가 쉽습니다.

c=0 인 이유는 v 노드를 기준으로 하기 때문에 c가 v노드일 때는 고려하지 않기 때문입니다.
v가 c일 때를 고려한다면 b가 되어버립니다.
Graphlet은 노드의 지역적 위상(node's local network topology)을 측정해주는 척도 입니다. 두 노드의 GDV를 비교하는 것은 그 노드 주변이 얼마나 비슷한지 (지역적 위상이 얼마나 비슷한지) 알려줍니다.
하나의 노드를 기준으로 고차원으로 구성된 벡터를 얻어낼 수 있기 때문에 노드를 특징화할 수 있고, 다양한 것에 활용해볼 수 있습니다.
3. Finding Motifs and Graphlets
어떻게 Motif와 Graphlet을 찾는지 알아보겠습니다. k개 노드에 대한 subgraph를 찾는 과제에는 2가지 단계를 거치는데 , 문제가 있습니다.
- Enumerating : size-k의 가능한 모든 subgraph를 찾는 과정
- Counting : 찾은 모든 subgraph의 occurance를 세는 과정
이 두 단계를 거치게 되는데 subgraph 수의 증가에 따라 exponential하게 계산량이 증가합니다. (계산 가능한 motif의 크기는 3~8개 정도로 매우 작음) -> NP-Problem
따라서 Enumerating 하는 알고리즘이 대표적으로 3개 있습니다. (완전탐색이 아닌 지식기반의 휴리스틱한 접근의 알고리즘)
- Exact subgraph enumeration (ESU) [Wernicke 2006] -> 오늘 배울 것!
- Kavosh [Kashani et al. 2009]
- Subgraph sampling [Kashtan et al. 2004]
Exact subgraph enumeration (ESU)
ESU 알고리즘은 v노드에서 시작해서 새로운 노드 u를 추가하면서 subgraph를 만들어가는 방법입니다. V_extension의 후보 노드가 V_subgraph로 이동하면서 state를 업데이트 하고 재귀적인 구조가 생깁니다.
그림을 보는 것이 이해가 쉽습니다.

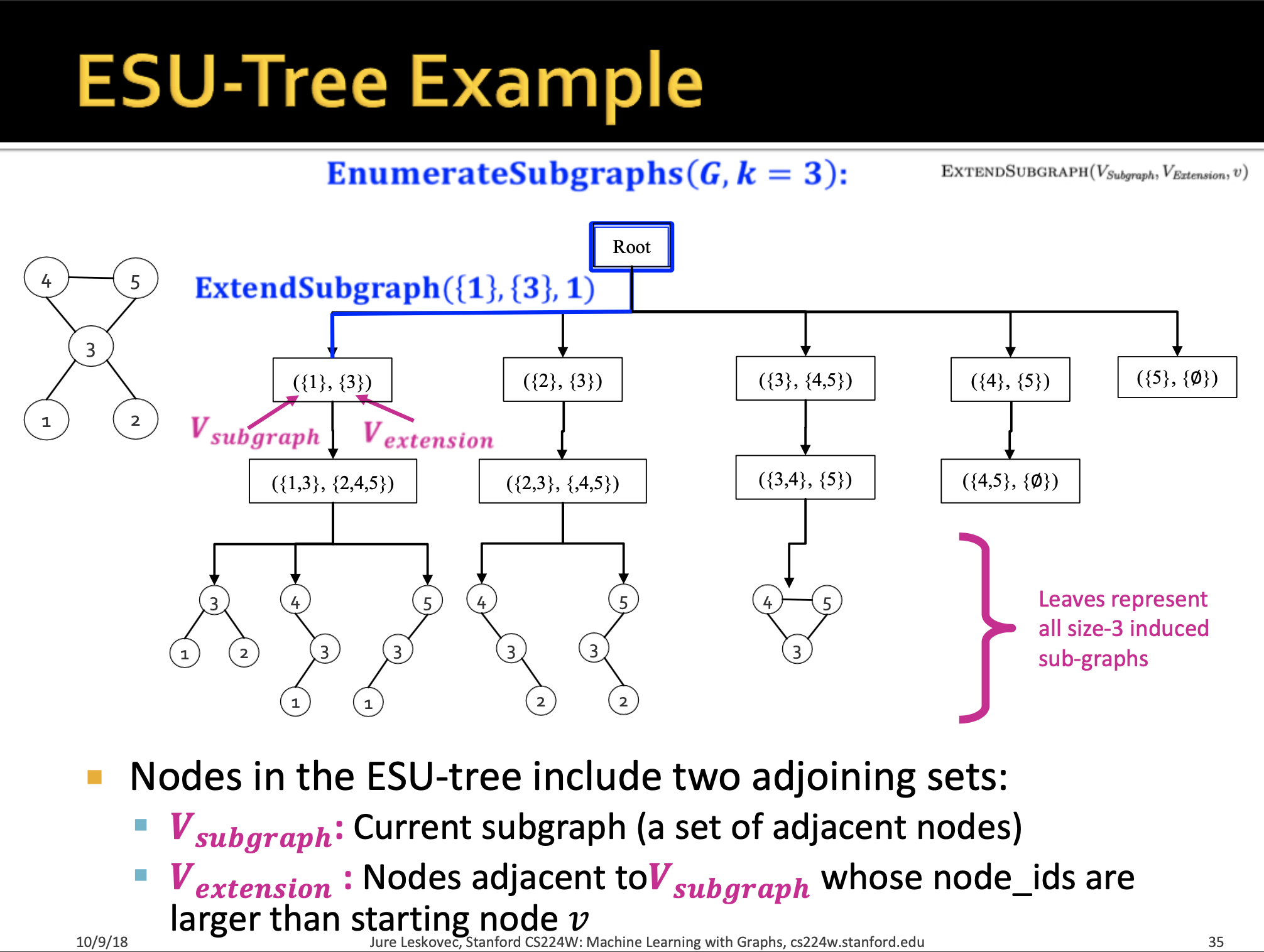
{{3},{4},{5}} 가 아니라 {{4},{5}} 인 이유는 인덱스 값이 extension의 것이 커야하기 때문입니다.

Counting
count를 하는 기준은 non-isomorphic한 graph를 토대로 subgraphs의 개수를 세주는 것입니다.
3개의 노드와 2개의 edge로 구성되어 있는 subgraph는 topologically equivalent한 isomorphic한 graph이기 때문에 해당 구조가 총 5번 나왔다고 할 수 있으며, 이 때 isomorphic을 구별하기 위해 Mckay's nauty algorithm을 사용했다고 합니다.
Graph Isomorphism


isomorphic에 대한 설명이 좀 늦었는데, 위상적으로 같다는 것입니다. 머그컵과 도넛이 같은 위상이라는 것... 모두 알고 있을겁니다. 여기서는 bijection일 때 G와 H는 같습니다. 그런데 이를 check 해보려면 9! 번 체크해야하고 computation problem 이 있습니다. 그래서 이를 한번에 찾을 수 있는 방법을 고안하다가 mapping하는 f를 찾아보자는 아이디어가 나옵니다.
4. Structural Roles in Networks


Role 이란 graph에서 노드의 function 입니다. 네트워크에서 비슷한 위치, 기능을 하는 노드의 집합을 의미하는 자료구조입니다. 커뮤니티나 그룹과는 다른 개념인데, 위의 예시보다 직관적으로 예를 들자면, 회사에는 인사팀과 개발팀이 있습니다. 이 둘은 같은 role 이라고 하지 않지만, 이 각 팀에는 같은 role을 가진 팀장들이 있습니다. (따라서 이 노드들 끼리 연결되어 있을 필요는 없습니다. 같은 community x)
Structural equivalance
similar position 혹은 similar structural properties로 네트워크 내의 Role을 판단하기 위해서 Structural equivalence라는 개념이 사용됩니다. Structural equivalence는 노드 U, V가 다른 노드와의 관계가 동일하다면 구조적으로 동등한 role로 볼 수 있음을 의미합니다.

Structural Roles 은 클러스터링을 통해 발견하는데, 이제 찾아내는 방법을 알아보겠습니다.
5. Discovering Structural Roles in Networks
role 에 대한 task 는 크게 6가지로 분류됩니다.
- Role query : 알려진 target 값과 비슷한 행동을 하는 individual 식별 (individual identify)
- Role outliers : 비정상적인 행동을 하는 individual 식별
- Role dynamics : 비정상적인 행동 변화 식별
- Identity resolution : 새로운 네트워크에서 식별 (Identify, de-anonymize, individuals in a new network)
- Role transfer : 한 네트워크에 대한 지식 사용해서 다른 네트워크에 대한 예측
- Network comparison : 네트워크 유사성 계산, 지식 전달을 위한 호환성 결정
task 들이 엄청 와닿지는 않았는데, Structural Role 을 발견하는 방법 중에 RolX 에 대해서 알아보겠습니다.
RolX

input -> output 모습
- 각 노드의 네트워크 구조상 role을 자동으로 찾아주는 방법
- unsupervised learning, 사전 정보를 요구하지 않음
- 각 노드에 mixture of roles 부여 (한 가지 role 만을 부여하지 않음)
- edge 수에 따라서 선형적으로 크기가 커짐

RolX 의 과정 중 하나인 Recursive Feature Extraction에 대해서 먼저 알아보겠습니다.
Recursive Feature Extraction


네트워크 연결성으로 구조적 feature를 만드는 것입니다.
기본 아이디어는 노드의 기능을 집계해서 새로운 recursive feature를 생성하는 것입니다. 노드의 이웃 feature 중에 기본적인 것 두가지를 소개합니다.
-
Local Features: 노드의 차수에 대한 모든 측정치
- 방향 그래프라면, include in- and out-degree, total degree
- 가중 그래프라면, include weighted feature versions
-
Egonet Features: 노드의 egonet에서 계산되는 값
- Egonet은 노드에서 유도된 subgraph의 노드와 이웃 그리고 모든 edges를 포함합니다.
기본 base set of features를 형성했으면 집계를 통해 feature를 추가해서 확장합니다. mean 이나 sum 과 같은 집계함수(통계량)을 사용합니다. 재귀를 돌 때마다 계산해야하는 features의 수가 exponential 하게 급증하기 때문에 pruning (가지치기)를 사용합니다.
-> pruning : 두 feature간에 correlated가 높으면 하나씩 제거해보면서 직접 threshold를 지정합니다.

최종적인 Role Extraction overview는 위와 같습니다.
(clustering에는 non negative matrix factorization / model selection 에는 MDL(minimum discription length, 최소설명 길이) / likelihood 측정에는 KL-divergence(쿨백-라이블러발산)을 사용합니다.
예시로는 '정치도서들이 함께 구매된 네트워크'를 보겠습니다.
- node : 아마존에 있는 정치도서
- edge : 같은 사람에게 책이 같이 구매되는 빈도

노드의 라벨(진보, 보수, 중립)이 주어지지 않았는데 알고리즘으로 어떤 노드가 central이고 peripheral인지 role을 구분했습니다. 맨처음 role에 대해 설명했던대로 각 클러스터에 비슷한 role을 가진 노드들이 분포하는 것을 볼 수 있습니다.
Reference
Stanford CS224W 2019
스터디 3강 리뷰 자료 velog.io/@tobigs-gnn1213/3.-Motifs-and-Structural-Roles-in-Networks
3. Motifs and Structural Roles in Networks
작성자 : 오진석Motifs and Structural Roles in NetworksSubgraphs, Motifs, and GraphletsGraphlets: Node feature vectorsFinding Motifs and GrphletsStructural R
velog.io
'🗂 REVIEW > Graph Study' 카테고리의 다른 글
| [CS224W] 5. Spectral Clustering (0) | 2021.03.08 |
|---|---|
| [CS224W] 4. Community Structure in Networks (0) | 2021.03.07 |
| [CS224W] 2. Properties of Networks and Random Graph Models (0) | 2021.02.12 |
| [CS224W] 1. Introduction; Structure of graph (0) | 2021.02.12 |
| ```시작하며``` (0) | 2021.02.12 |
