딥러닝에서 선형변환의 기하학적 의미
Linear Transformation in Neural Networks
딥러닝에서 선형변환의 기하학적 의미는 다음과 같이 시각화한 gif 로 한장으로 볼 수 있다.
원래의 모눈종이가 standard basis들이라고 하면 ([1,0].T , [0,1].T)
모눈종이가 점점 기울어진 평행사변형이 되는 것이 linear transform (선형변환) 이고,
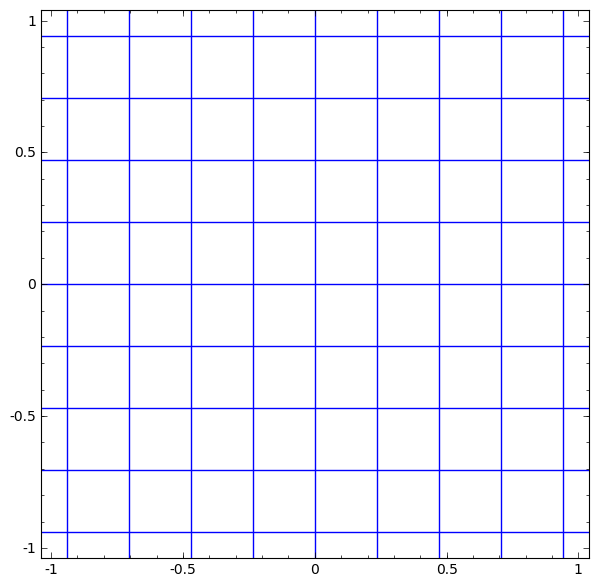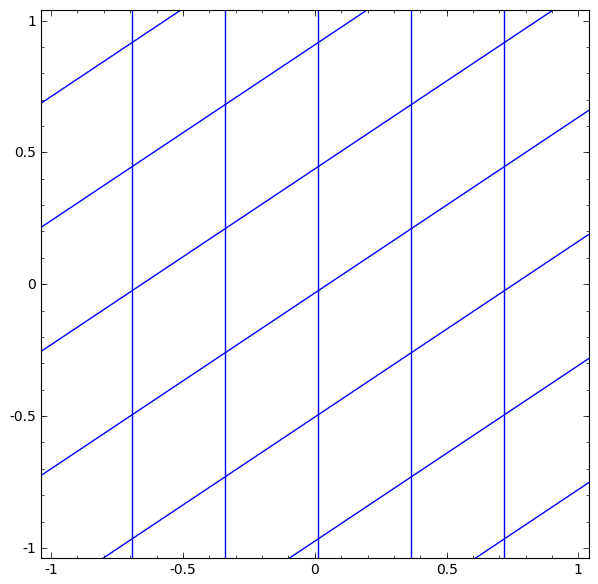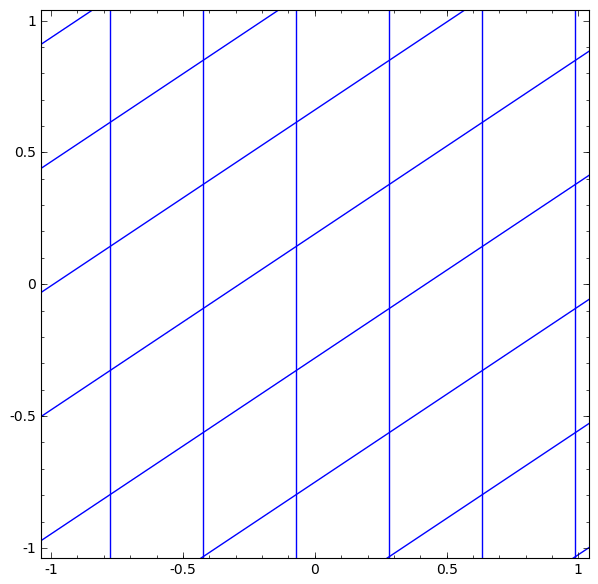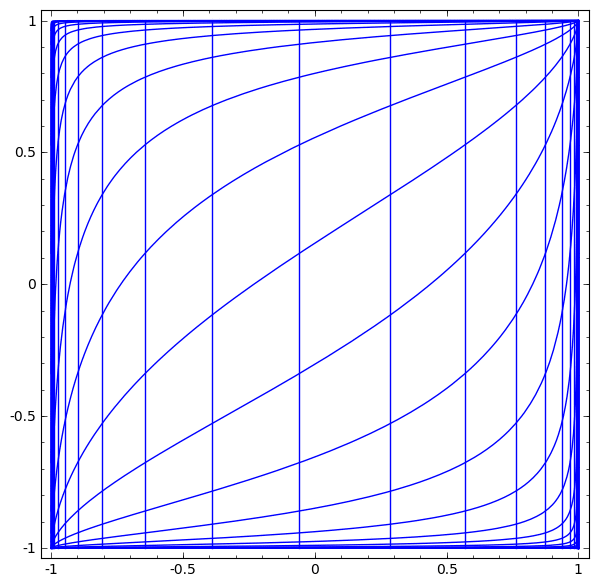
곡선으로 꾸겨지는 부분은 non linear 함수를 사용했을 때의 모습이다.
(이 때 0 부분은 거의 그대로 유지되는 모숩을 볼 수 있다.)
흐르는 것은 bias 를 표현한 것이다.
이러한 일련의 과정이 딥러닝의 node에서 이루어지고 있는 모습을 시각화 한 것이다.
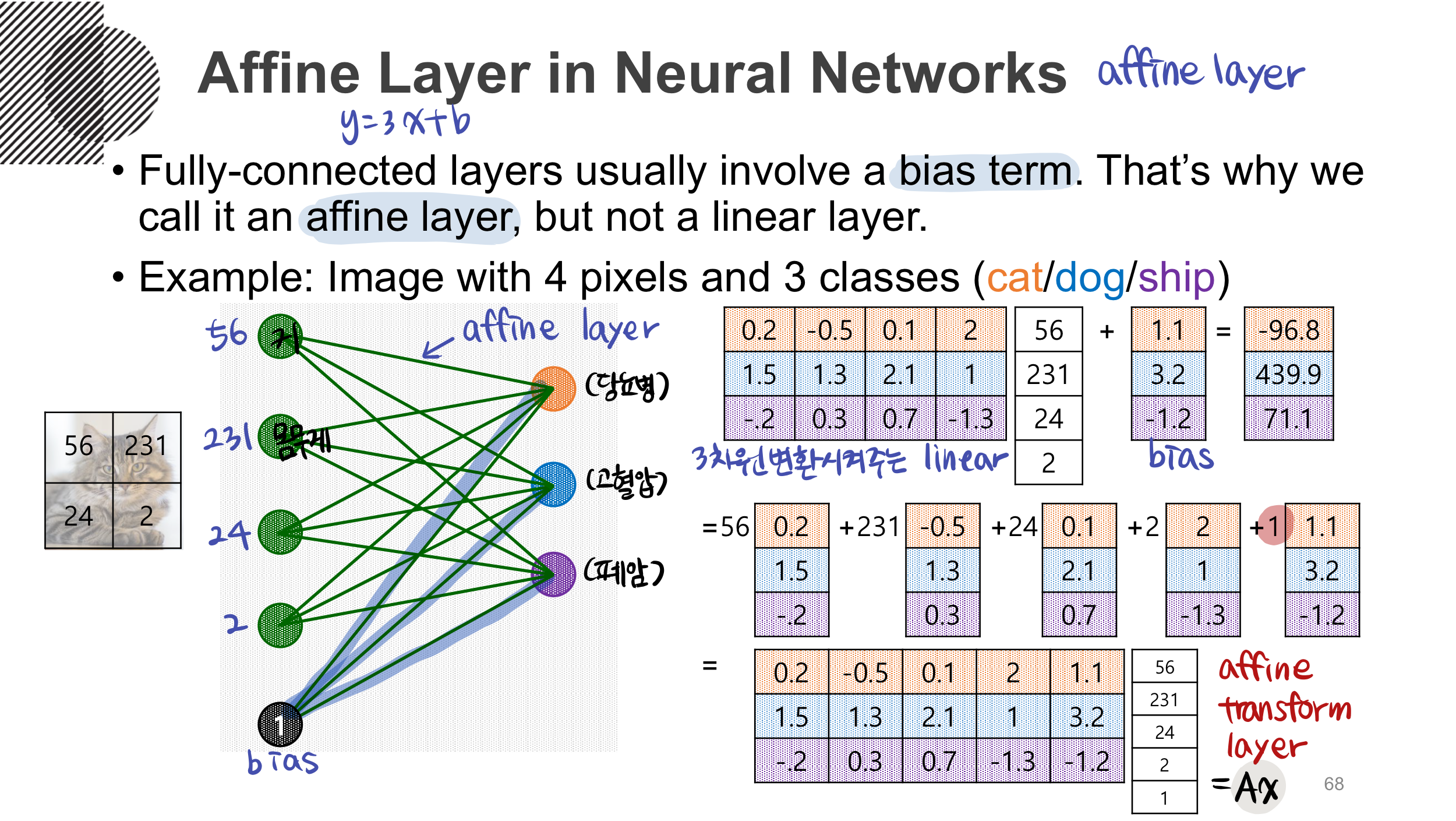
Affine Layer
추가로 bias 를 포함한 y = ax + b 등의 식은 선형결합이 되지 않는데,
이를 선형결합으로 만들어 주기 위해서는 [a b] [x 1].T 로 다시 쓰면 된다.
따라서 딥러닝에서 bias 를 포함한 layer 는 linear layer 가 아니라 affine layer (affine transform layer) 라고 부르게 되는데 다음 ppt 이미지 처럼 1이라는 scalar 를 bias vector 에 곱한다.
(필기 때문에 알아보기 구릴 수 있지만, 3개의 클래스로 분류하는 과정을 나타낸다.)
Reference
colah.github.io/posts/2014-03-NN-Manifolds-Topology/
주재걸 교수님의 인공지능을 위한 선형대수
'🤖 Today-I-Learned ] > Statistics & Machine Learning' 카테고리의 다른 글
| [선형대수] Orthogonal Projection ŷ of y (0) | 2021.01.26 |
|---|---|
| [선형대수] 딥러닝에서의 일대일 대응 (ONE-TO-ONE) (0) | 2021.01.25 |
| [선형대수] 머신러닝에서 Rank of Matrix 의 의미 (0) | 2021.01.22 |
| [MLE] Erlang분포(gamma분포)의 최대우도추정량 (0) | 2020.10.02 |
| [경제자료분석] 2019-2학기 경제자료분석 (0) | 2020.05.03 |
딥러닝에서 선형변환의 기하학적 의미
Linear Transformation in Neural Networks
딥러닝에서 선형변환의 기하학적 의미는 다음과 같이 시각화한 gif 로 한장으로 볼 수 있다.
원래의 모눈종이가 standard basis들이라고 하면 ([1,0].T , [0,1].T)
모눈종이가 점점 기울어진 평행사변형이 되는 것이 linear transform (선형변환) 이고,
곡선으로 꾸겨지는 부분은 non linear 함수를 사용했을 때의 모습이다.
(이 때 0 부분은 거의 그대로 유지되는 모숩을 볼 수 있다.)
흐르는 것은 bias 를 표현한 것이다.
이러한 일련의 과정이 딥러닝의 node에서 이루어지고 있는 모습을 시각화 한 것이다.

Affine Layer
추가로 bias 를 포함한 y = ax + b 등의 식은 선형결합이 되지 않는데,
이를 선형결합으로 만들어 주기 위해서는 [a b] [x 1].T 로 다시 쓰면 된다.
따라서 딥러닝에서 bias 를 포함한 layer 는 linear layer 가 아니라 affine layer (affine transform layer) 라고 부르게 되는데 다음 ppt 이미지 처럼 1이라는 scalar 를 bias vector 에 곱한다.
(필기 때문에 알아보기 구릴 수 있지만, 3개의 클래스로 분류하는 과정을 나타낸다.)

Reference
colah.github.io/posts/2014-03-NN-Manifolds-Topology/
주재걸 교수님의 인공지능을 위한 선형대수
'🤖 Today-I-Learned ] > Statistics & Machine Learning' 카테고리의 다른 글
| [선형대수] Orthogonal Projection ŷ of y (0) | 2021.01.26 |
|---|---|
| [선형대수] 딥러닝에서의 일대일 대응 (ONE-TO-ONE) (0) | 2021.01.25 |
| [선형대수] 머신러닝에서 Rank of Matrix 의 의미 (0) | 2021.01.22 |
| [MLE] Erlang분포(gamma분포)의 최대우도추정량 (0) | 2020.10.02 |
| [경제자료분석] 2019-2학기 경제자료분석 (0) | 2020.05.03 |
