Orthogonal Projection ŷ of y (y의 정사영 y-hat)
y의 Orthogonal Projection 값 ŷ 을 구하는 방법을 알아보자.
1. [2차원에서의 설명] Orthogonal Projection ŷ of y onto Line
Line L에 Orthogonal projection (사영) 시키는 경우는 다음과 같다.
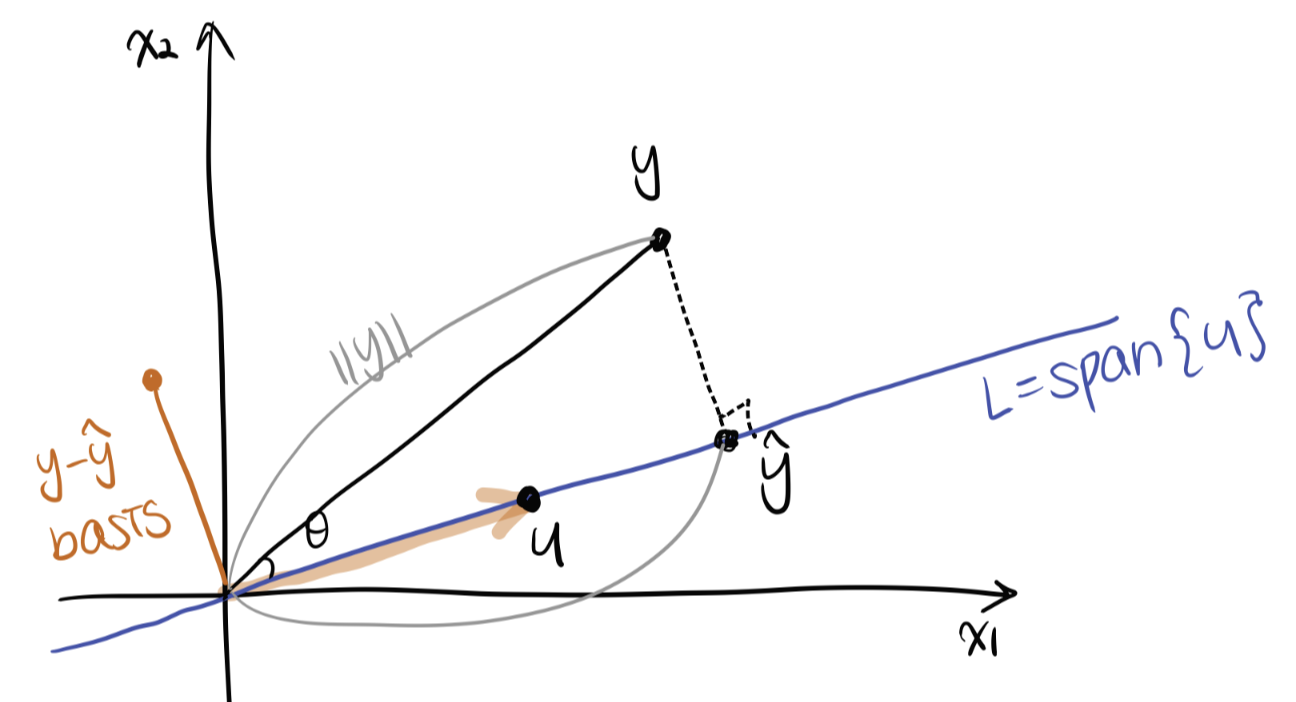

ŷ 의 값을 구하기 위해서는 ŷ 의 길이와 ŷ 의 방향을 곱한다.
- y의 길이는 y norm 이다. (||y||)
- ŷ 의 길이는 ||y|| cosθ이기 때문에 y와 u의 내적에서 유도한다.
- 방향은 u 벡터의 방향에서 유도한다. u 의 unit vector(단위벡터) 를 구하면, 길이는 1이면서 방향만 남는다.
- 길이 x 방향 을 해주면 2번과 3번을 곱한다.
- 만약 u가 길이 1인 단위 벡터였다면 y-hat은 (y · u) u 이다.
basis는 y - ŷ 을 원점으로 이동시킨 벡터로 나타낼 수 있다.
실제 숫자를 대입해서 구하는 과정을 나타내면 다음과 같이 좀 더 와닿는다.

항상 공식을 기억하고 있자.
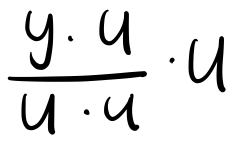
2. [3차원에서의 설명] Orthogonal Projection ŷ of y onto Plane
span 이 palane (평면) 으로, subspace W 에 Orthogonal projection 시키는 경우다.
따라서 span = {u1, u2} 이다.
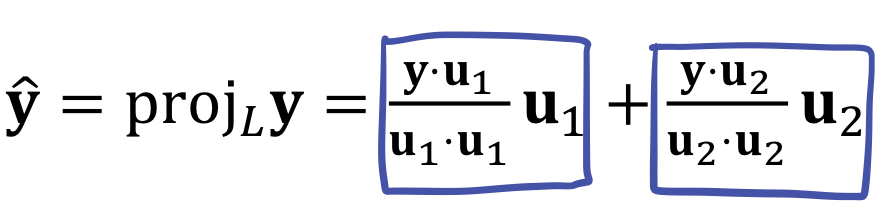
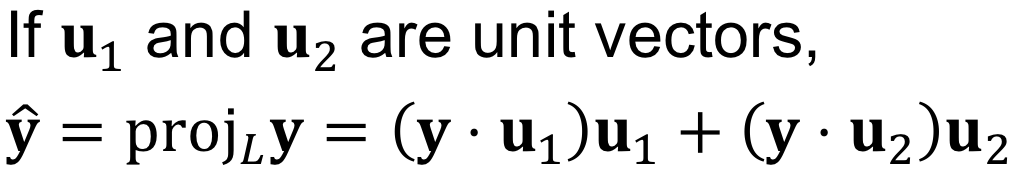
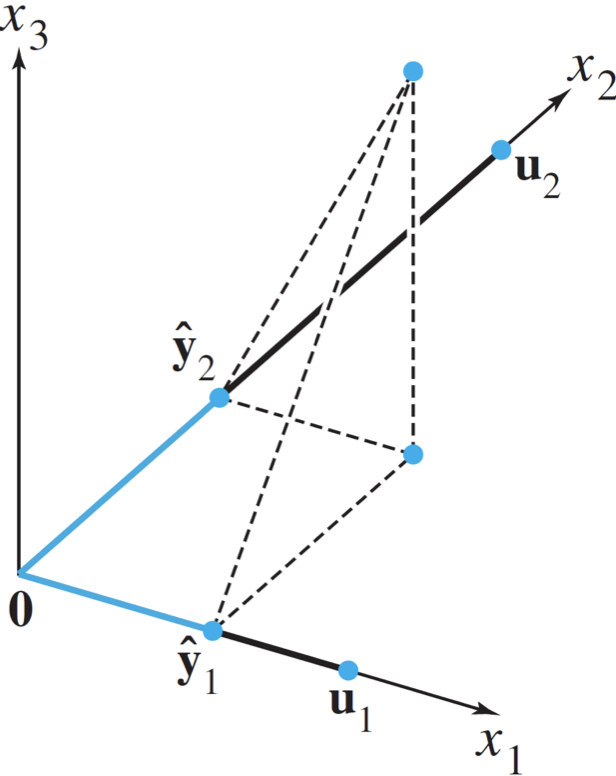
고차원으로 가는 경우는 y를 u1 에 사영 시키는 경우와 u2 에 사영 시키는 경우를 더한 값이 된다. 즉 각 basis 벡터별로 사영시킨 후에 더하면 된다.
이는 삼수선의 정리를 사용해서 증명 가능한데, 생략한다.
(이 때 만약 y가 이미 subspace W에 포함되어 있는 경우라면 orthogonal projection 은 자기 자신이 된다.)
그런데 지금까지의 Orthogonal Projection이 Machine Learning 에도 필요한 개념 일까? 이 부분은 다음 포스팅에 이어서 설명하겠다.
Reference
주재걸 교수님의 인공지능을 위한 선형대수
반응형
'🤖 Today-I-Learned ] > Statistics & Machine Learning' 카테고리의 다른 글
| [선형대수] 그람-슈미트 직교화 (Gram–Schmidt Orthogonalization) (2) | 2021.02.01 |
|---|---|
| [선형대수] 다중공선성 (Multicollinearity) 의 기하학적 의미 (0) | 2021.01.26 |
| [선형대수] 딥러닝에서의 일대일 대응 (ONE-TO-ONE) (0) | 2021.01.25 |
| [선형대수] 딥러닝에서 선형변환의 기하학적 의미 (2) | 2021.01.24 |
| [선형대수] 머신러닝에서 Rank of Matrix 의 의미 (0) | 2021.01.22 |
