다중공선성 (Multicollinearity) / correlation 의 기하학적 의미
머신러닝 모델을 만들 때 흔히 발생하는 문제 중 하나가 다중공선성이다. 그렇다면 다중공선성, 즉 변수간의 correlation이 높다는 것은 어떤 뜻이고 어떤 문제를 야기할까?
이 글은 저번 Orthogonal Projection 과 이어진다.
2021/01/26 - [[ Today I Learned ]/Linear algebra] - [선형대수] Orthogonal Projection ŷ of y
[선형대수] Orthogonal Projection ŷ of y
Orthogonal Projection ŷ of y, (y의 정사영 y-hat) y의 Orthogonal Projection 값 ŷ 을 구하는 방법을 알아보자. 1. [2차원에서의 설명] Orthogonal Projection ŷ of y onto Line Line L에 Orthogona..
jxnjxn.tistory.com
보통 우리가 가진 데이터의 변수, feature (variable) 들은 orthogonal 하지 않은 관계가 더 많을 것이다.
그런데 projection에서 orthogonal 이 아닌 경우, projection 시에 다른 벡터의 영향을 받는다. 이 성질은 두 피쳐의 성질이 비슷 한 경우 (correalation) 이 높은 경우에 기하학적으로 큰 파장을 야기한다.
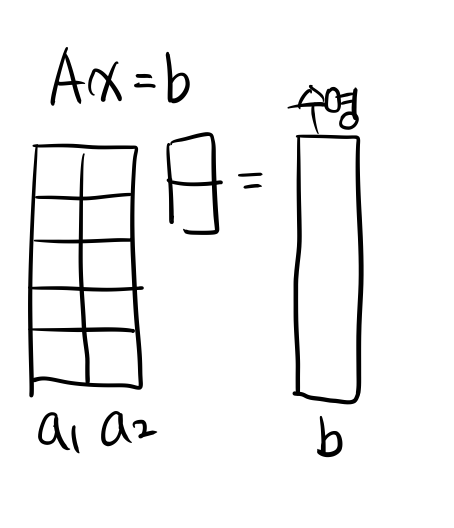
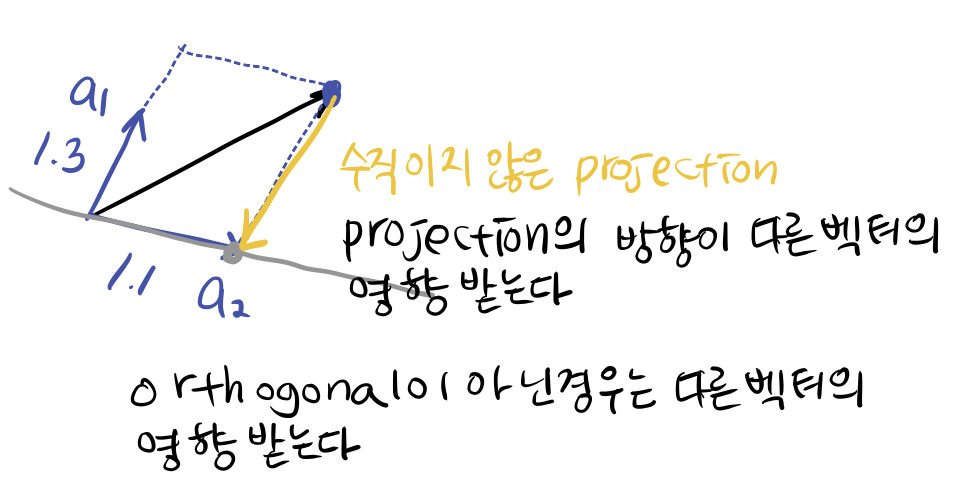
아래의 그림을 머리에 넣도록 하자. 그림이 모든 것을 설명해준다.
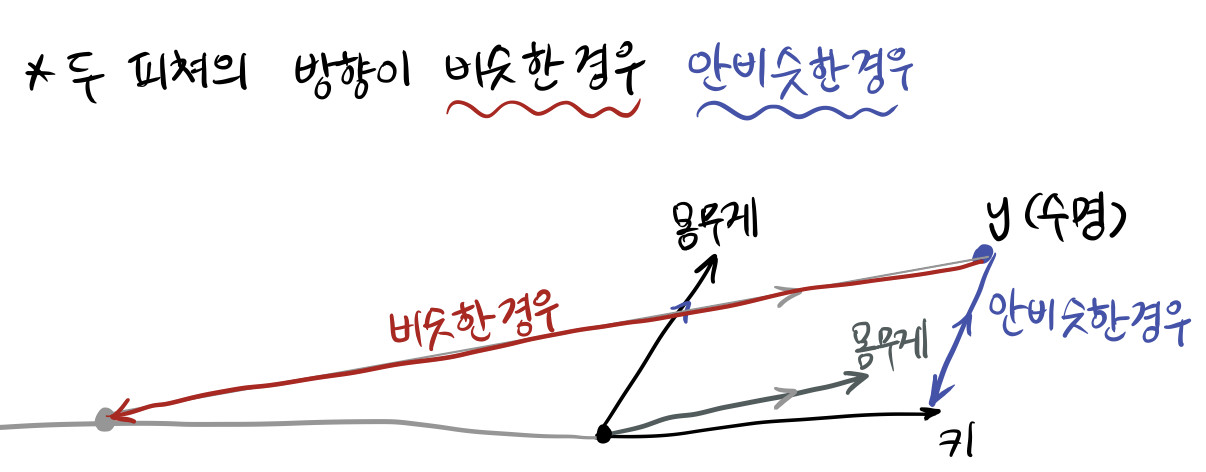
가장 오차가 적을 때는 y에서 Orthogonal 하게 Projection 할 때이다. (수선의 발을 내릴 때이다. 90도)
파란색은 몸무게와 키 피쳐가 방향이 비슷하지 않은 경우이다. Orthogonal Projection 은 아니지만 y 에서 직선으로 수선의 발을 내렸을 때와 비슷하게는 사영될 수 있다.
그런데 빨간색인 경우를 보자. 키 피쳐와 비슷한 방향으로 몸무게 백터가 존재할 경우, 평행한 직선을 사영시키기 위해서 굉장히 멀리까지 평행한 선을 그려줘야한다.
이 때는 오차가 두 개의 계수 값을 크게 좌지우지 하게 된다. 두 피쳐의 방향이 비슷하다는 것은 correlation을 가지는 경우인데, 즉 변수간의 correlation이 있으면 Linear Regression (머신러닝 모델) 의 성능이 민감 해 진다는 것을 의미한다.
민감해진 모델은 unseen data, 모델이 train 시에 보지 못한 데이터에 대해서 성능이 떨어진다. (Overfitting 된다.)
그래서 머신러닝 모델은 변수간의 상관성이 큰 경우를 싫어했던 것이다.
이를 해결하기 위해서는 regularization ( L1, L2 )을 사용한다.
Reference
주재걸 교수님의 인공지능을 위한 선형대수
'🤖 Today-I-Learned ] > Statistics & Machine Learning' 카테고리의 다른 글
| [선형대수] QR분해 (QR Factorization) (0) | 2021.02.02 |
|---|---|
| [선형대수] 그람-슈미트 직교화 (Gram–Schmidt Orthogonalization) (2) | 2021.02.01 |
| [선형대수] Orthogonal Projection ŷ of y (0) | 2021.01.26 |
| [선형대수] 딥러닝에서의 일대일 대응 (ONE-TO-ONE) (0) | 2021.01.25 |
| [선형대수] 딥러닝에서 선형변환의 기하학적 의미 (2) | 2021.01.24 |
다중공선성 (Multicollinearity) / correlation 의 기하학적 의미
머신러닝 모델을 만들 때 흔히 발생하는 문제 중 하나가 다중공선성이다. 그렇다면 다중공선성, 즉 변수간의 correlation이 높다는 것은 어떤 뜻이고 어떤 문제를 야기할까?
이 글은 저번 Orthogonal Projection 과 이어진다.
2021/01/26 - [[ Today I Learned ]/Linear algebra] - [선형대수] Orthogonal Projection ŷ of y
[선형대수] Orthogonal Projection ŷ of y
Orthogonal Projection ŷ of y, (y의 정사영 y-hat) y의 Orthogonal Projection 값 ŷ 을 구하는 방법을 알아보자. 1. [2차원에서의 설명] Orthogonal Projection ŷ of y onto Line Line L에 Orthogona..
jxnjxn.tistory.com
보통 우리가 가진 데이터의 변수, feature (variable) 들은 orthogonal 하지 않은 관계가 더 많을 것이다.
그런데 projection에서 orthogonal 이 아닌 경우, projection 시에 다른 벡터의 영향을 받는다. 이 성질은 두 피쳐의 성질이 비슷 한 경우 (correalation) 이 높은 경우에 기하학적으로 큰 파장을 야기한다.


아래의 그림을 머리에 넣도록 하자. 그림이 모든 것을 설명해준다.

가장 오차가 적을 때는 y에서 Orthogonal 하게 Projection 할 때이다. (수선의 발을 내릴 때이다. 90도)
파란색은 몸무게와 키 피쳐가 방향이 비슷하지 않은 경우이다. Orthogonal Projection 은 아니지만 y 에서 직선으로 수선의 발을 내렸을 때와 비슷하게는 사영될 수 있다.
그런데 빨간색인 경우를 보자. 키 피쳐와 비슷한 방향으로 몸무게 백터가 존재할 경우, 평행한 직선을 사영시키기 위해서 굉장히 멀리까지 평행한 선을 그려줘야한다.
이 때는 오차가 두 개의 계수 값을 크게 좌지우지 하게 된다. 두 피쳐의 방향이 비슷하다는 것은 correlation을 가지는 경우인데, 즉 변수간의 correlation이 있으면 Linear Regression (머신러닝 모델) 의 성능이 민감 해 진다는 것을 의미한다.
민감해진 모델은 unseen data, 모델이 train 시에 보지 못한 데이터에 대해서 성능이 떨어진다. (Overfitting 된다.)
그래서 머신러닝 모델은 변수간의 상관성이 큰 경우를 싫어했던 것이다.
이를 해결하기 위해서는 regularization ( L1, L2 )을 사용한다.
Reference
주재걸 교수님의 인공지능을 위한 선형대수
'🤖 Today-I-Learned ] > Statistics & Machine Learning' 카테고리의 다른 글
| [선형대수] QR분해 (QR Factorization) (0) | 2021.02.02 |
|---|---|
| [선형대수] 그람-슈미트 직교화 (Gram–Schmidt Orthogonalization) (2) | 2021.02.01 |
| [선형대수] Orthogonal Projection ŷ of y (0) | 2021.01.26 |
| [선형대수] 딥러닝에서의 일대일 대응 (ONE-TO-ONE) (0) | 2021.01.25 |
| [선형대수] 딥러닝에서 선형변환의 기하학적 의미 (2) | 2021.01.24 |
