QR분해 (QR Factorization)
그람-슈미트 직교화에서 orthogonal한 벡터를 주고 다시 원래의 벡터를 찾는 것을 matrix factorization, input matrix 복원이라고 언급했다. 이번 글에서는 이 QR Factorization을 설명한다.
1. 그람-슈미트 직교화를 설명한 예제에서 basis를 찾은 모습은 다음과 같다. 선형결합의 꼴로 나타낼 수 있다.
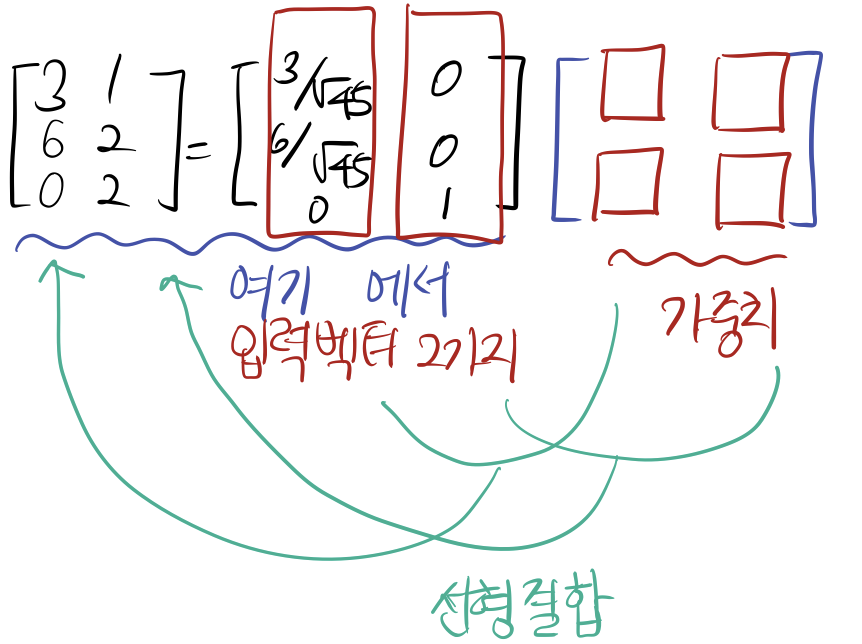
원래의 벡터가 basis와 다른 matrix로 선형결합꼴이 된다.
왼쪽의 벡터가 주어진 basis 이고 입력벡터, 오른쪽을 가중치로 볼 수 있다.
2. 여기서 ㅁ 를 채우는 방법 = 가중치(weight)를 구하는 방법이다.

basis 두 가지 중에 제일 첫번째 벡터는 단순히 원래 벡터의 normarlize 로 구했기 때문에 이 벡터만으로도 원래의 벡터를 복원 가능하다.
-> 따라서 1번, 2번에 대해서 채울 수 있다.
하지만 그 다음 원래의 벡터 [1,2,2].T 는 원래의 normarlize로 구한 basis와 [0,0,1].T의 선형결합으로 이루어져 있다.
-> 3번, 4번을 채우기 위해서는 한 개의 벡터가 아니라 이 전의 벡터를 참고 해야한다.
3. 다시 이 과정들 (그람-슈미트 직교화에서 나온 과정) 을 정리, 시각화 하면 다음 그림이다.
기존 벡터가 4개 이상일 떄의 모습이다.
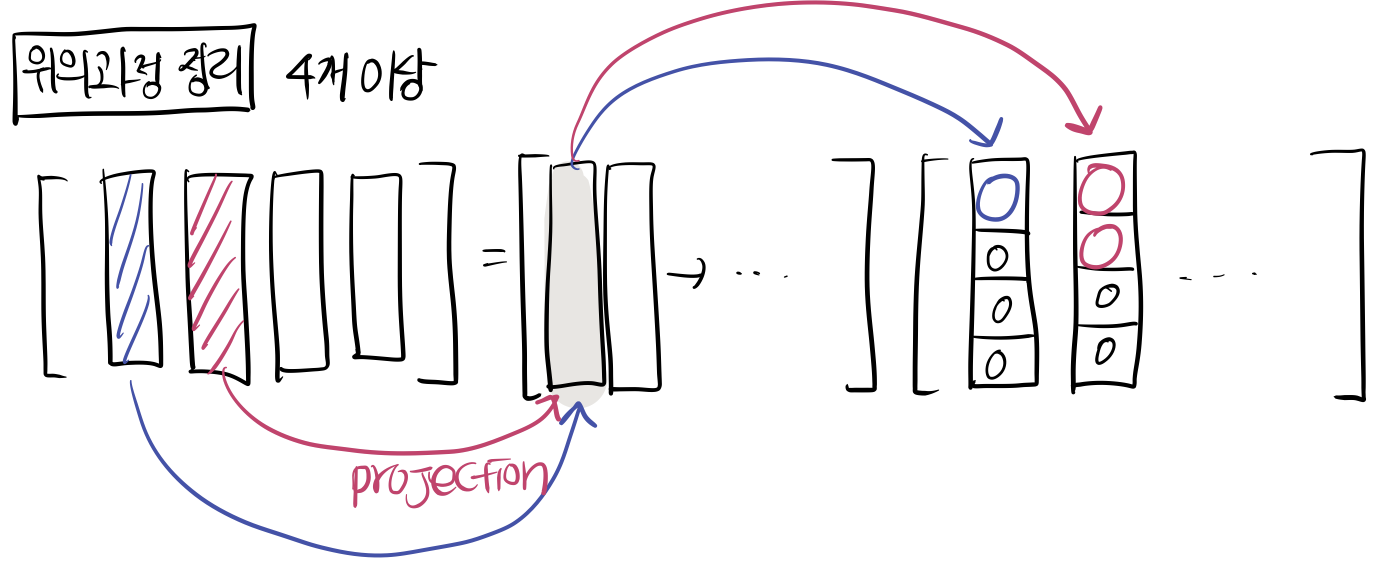
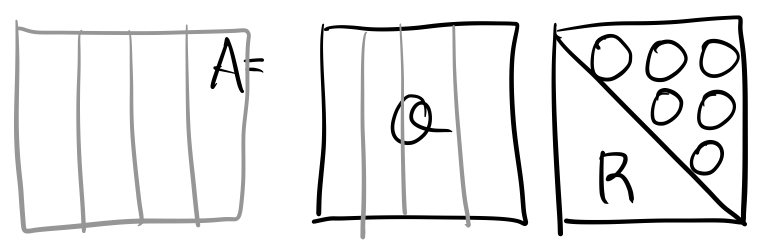
오른쪽의 matrix를 보면 원소가 upper triangular matrix로 있는 모습을 발견할 수 있다.
즉 A라는 matrix는 다음과 같은 Q 와 R의 matrix 로 분해된다.
A는 linearly independent한 column을 가지는 matrix, Q는 동일한 column 갯수를 가지고 orthonormal한 basis를 가지는 matrix, R은 upper triangular matrix 형태이다. (0으로 채워지지 않은 원소가 선형결합의 계수로 쓰임, 가중치)
이 꼴로 분해 되는 것을 QR 분해, QR Factorization 이라고 한다.
Reference
주재걸 교수님의 인공지능을 위한 선형대수
'🤖 Today-I-Learned ] > Statistics & Machine Learning' 카테고리의 다른 글
| [선형대수] Null Space 와 Orthogonal Complement (4) | 2021.02.21 |
|---|---|
| [선형대수] 고유값과 고유벡터 (eigenvector & eigenvalue) (0) | 2021.02.12 |
| [선형대수] 그람-슈미트 직교화 (Gram–Schmidt Orthogonalization) (2) | 2021.02.01 |
| [선형대수] 다중공선성 (Multicollinearity) 의 기하학적 의미 (0) | 2021.01.26 |
| [선형대수] Orthogonal Projection ŷ of y (0) | 2021.01.26 |
QR분해 (QR Factorization)
그람-슈미트 직교화에서 orthogonal한 벡터를 주고 다시 원래의 벡터를 찾는 것을 matrix factorization, input matrix 복원이라고 언급했다. 이번 글에서는 이 QR Factorization을 설명한다.
1. 그람-슈미트 직교화를 설명한 예제에서 basis를 찾은 모습은 다음과 같다. 선형결합의 꼴로 나타낼 수 있다.

원래의 벡터가 basis와 다른 matrix로 선형결합꼴이 된다.
왼쪽의 벡터가 주어진 basis 이고 입력벡터, 오른쪽을 가중치로 볼 수 있다.
2. 여기서 ㅁ 를 채우는 방법 = 가중치(weight)를 구하는 방법이다.

basis 두 가지 중에 제일 첫번째 벡터는 단순히 원래 벡터의 normarlize 로 구했기 때문에 이 벡터만으로도 원래의 벡터를 복원 가능하다.
-> 따라서 1번, 2번에 대해서 채울 수 있다.
하지만 그 다음 원래의 벡터 [1,2,2].T 는 원래의 normarlize로 구한 basis와 [0,0,1].T의 선형결합으로 이루어져 있다.
-> 3번, 4번을 채우기 위해서는 한 개의 벡터가 아니라 이 전의 벡터를 참고 해야한다.
3. 다시 이 과정들 (그람-슈미트 직교화에서 나온 과정) 을 정리, 시각화 하면 다음 그림이다.
기존 벡터가 4개 이상일 떄의 모습이다.


오른쪽의 matrix를 보면 원소가 upper triangular matrix로 있는 모습을 발견할 수 있다.
즉 A라는 matrix는 다음과 같은 Q 와 R의 matrix 로 분해된다.
A는 linearly independent한 column을 가지는 matrix, Q는 동일한 column 갯수를 가지고 orthonormal한 basis를 가지는 matrix, R은 upper triangular matrix 형태이다. (0으로 채워지지 않은 원소가 선형결합의 계수로 쓰임, 가중치)
이 꼴로 분해 되는 것을 QR 분해, QR Factorization 이라고 한다.
Reference
주재걸 교수님의 인공지능을 위한 선형대수
'🤖 Today-I-Learned ] > Statistics & Machine Learning' 카테고리의 다른 글
| [선형대수] Null Space 와 Orthogonal Complement (4) | 2021.02.21 |
|---|---|
| [선형대수] 고유값과 고유벡터 (eigenvector & eigenvalue) (0) | 2021.02.12 |
| [선형대수] 그람-슈미트 직교화 (Gram–Schmidt Orthogonalization) (2) | 2021.02.01 |
| [선형대수] 다중공선성 (Multicollinearity) 의 기하학적 의미 (0) | 2021.01.26 |
| [선형대수] Orthogonal Projection ŷ of y (0) | 2021.01.26 |
