[선형대수] Null Space 와 Orthogonal Complement
Null Space(영공간) 과 Orthogonal Complement(직교여집합) 에 대해서 공부한 내용이다.
Null Space
정의
선형 방정식 Ax=b에서 b가 zero vector(=Null vector, =0벡터) 일때 식을 만족시키는 모든 가능한 해 x에 대한 집합이다.
-> 선형방정식 Ax=0의 해(Solutions)들이 이루는 공간, Null Space를 의미한다.
저번 시간 언젠가, 'Col A : A 의 column에 의해 span 이 되는 space' 라고 정의했다. (직사각행렬 가능)
비슷하게, Nul A 도 Null space of A 로 linear system 에서 Ax=0 을 만족하는 해들의 집합으로 이해하면 된다.
어떻게 찾을 것인가
특정 조건을 만족하면 되는데, row vector 들에 모두 수직은 각도를 가지는 해(x) 를 찾으면 된다. 그 해를 모은 집합이 null space !

이를 정리해서 수식으로 나타내면 이 조건을 이렇게 표현한다.
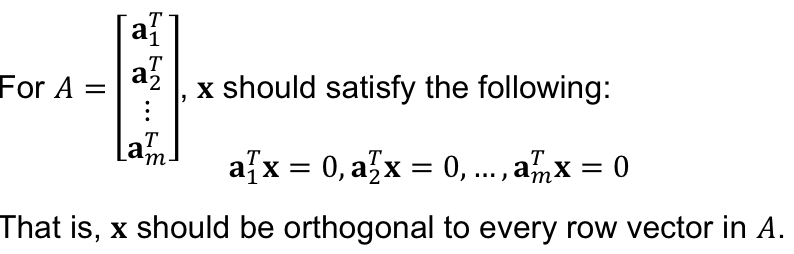
잠깐 예시를 보자, 위의 matrix 를 예시로 보자.
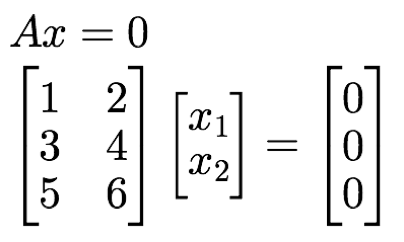
[[1,2],[3,4],[5,6]] 이 행렬에서 [x1,x2] = [0,0] 이 아닌
non-trivial solution 이 있을까? 없다!
column 들이 linearly independent 하기 때문이다. 하지만 이경우에도 Nul A 가 있긴 한데, Nul A = {0} 이다. ([0,0].T 인경우)
따라서 모든 matrix는 null space 로 0 벡터를 가지고 있다.
Orthogonal Complement

Null Space 를 찾는 예시를 보자.
ex) matrix A 의 Null space 를 따지고 Null space A의 dimenstion 을 구한다.
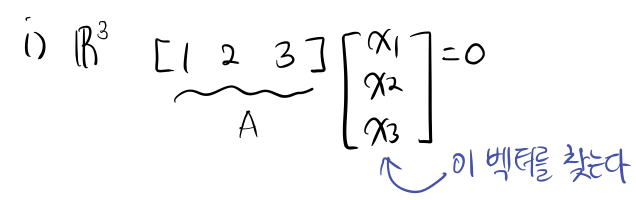
- A = [1,2,3] 이라는 matrix는 3차원의 공간에서 3차원의 해를 찾고 있다.
- 먼저, [1,2,3]과 linearly independent한 벡터를 찾는다.
- Gram-Schmidt로 orthogonal 한 벡터로 만들어준다.
즉 3차원에서 [1 2 3] 에 linearly independent한 벡터 찾아서 orthogonal한 벡터로 만들면 A와 새로운 벡터가 만드는 span이 있을 것이다. 이 때 하나의 벡터를 더 찾으면, 3차원 공간을 모두 커버하게 된다.
이 과정에서 [1 2 3] subspace의 dimension은 span{[1 2 3].T} -> 1-dim 이라고 하고, Nul A 의 basis는 3-1=2개 찾을 수 있다고 말한다. 이 것이 Rank Theorem 이다. 그리고 이렇게 양분되는 관계이기 때문에 Orthogonal Complement 라고 한다.
Rank Theorem
3 = dim RowA + dim Nul A = 1 + 2

(+ subspace는 선형결합에 닫혀있는가로 알 수 있다.)
Reference
주재걸 교수님의 인공지능을 위한 선형대수
'🤖 Today-I-Learned ] > Statistics & Machine Learning' 카테고리의 다른 글
| Hölder's inequality 증명 (0) | 2021.05.27 |
|---|---|
| [선형대수] 고유값과 고유벡터 (eigenvector & eigenvalue) (0) | 2021.02.12 |
| [선형대수] QR분해 (QR Factorization) (0) | 2021.02.02 |
| [선형대수] 그람-슈미트 직교화 (Gram–Schmidt Orthogonalization) (2) | 2021.02.01 |
| [선형대수] 다중공선성 (Multicollinearity) 의 기하학적 의미 (0) | 2021.01.26 |
[선형대수] Null Space 와 Orthogonal Complement
Null Space(영공간) 과 Orthogonal Complement(직교여집합) 에 대해서 공부한 내용이다.
Null Space
정의
선형 방정식 Ax=b에서 b가 zero vector(=Null vector, =0벡터) 일때 식을 만족시키는 모든 가능한 해 x에 대한 집합이다.
-> 선형방정식 Ax=0의 해(Solutions)들이 이루는 공간, Null Space를 의미한다.
저번 시간 언젠가, 'Col A : A 의 column에 의해 span 이 되는 space' 라고 정의했다. (직사각행렬 가능)
비슷하게, Nul A 도 Null space of A 로 linear system 에서 Ax=0 을 만족하는 해들의 집합으로 이해하면 된다.
어떻게 찾을 것인가
특정 조건을 만족하면 되는데, row vector 들에 모두 수직은 각도를 가지는 해(x) 를 찾으면 된다. 그 해를 모은 집합이 null space !

이를 정리해서 수식으로 나타내면 이 조건을 이렇게 표현한다.
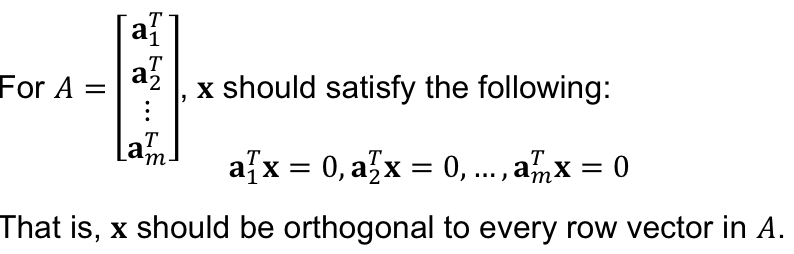
잠깐 예시를 보자, 위의 matrix 를 예시로 보자.
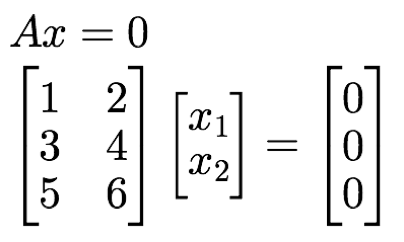
[[1,2],[3,4],[5,6]] 이 행렬에서 [x1,x2] = [0,0] 이 아닌
non-trivial solution 이 있을까? 없다!
column 들이 linearly independent 하기 때문이다. 하지만 이경우에도 Nul A 가 있긴 한데, Nul A = {0} 이다. ([0,0].T 인경우)
따라서 모든 matrix는 null space 로 0 벡터를 가지고 있다.
Orthogonal Complement

Null Space 를 찾는 예시를 보자.
ex) matrix A 의 Null space 를 따지고 Null space A의 dimenstion 을 구한다.

- A = [1,2,3] 이라는 matrix는 3차원의 공간에서 3차원의 해를 찾고 있다.
- 먼저, [1,2,3]과 linearly independent한 벡터를 찾는다.
- Gram-Schmidt로 orthogonal 한 벡터로 만들어준다.
즉 3차원에서 [1 2 3] 에 linearly independent한 벡터 찾아서 orthogonal한 벡터로 만들면 A와 새로운 벡터가 만드는 span이 있을 것이다. 이 때 하나의 벡터를 더 찾으면, 3차원 공간을 모두 커버하게 된다.
이 과정에서 [1 2 3] subspace의 dimension은 span{[1 2 3].T} -> 1-dim 이라고 하고, Nul A 의 basis는 3-1=2개 찾을 수 있다고 말한다. 이 것이 Rank Theorem 이다. 그리고 이렇게 양분되는 관계이기 때문에 Orthogonal Complement 라고 한다.
Rank Theorem
3 = dim RowA + dim Nul A = 1 + 2

(+ subspace는 선형결합에 닫혀있는가로 알 수 있다.)
Reference
주재걸 교수님의 인공지능을 위한 선형대수
'🤖 Today-I-Learned ] > Statistics & Machine Learning' 카테고리의 다른 글
| Hölder's inequality 증명 (0) | 2021.05.27 |
|---|---|
| [선형대수] 고유값과 고유벡터 (eigenvector & eigenvalue) (0) | 2021.02.12 |
| [선형대수] QR분해 (QR Factorization) (0) | 2021.02.02 |
| [선형대수] 그람-슈미트 직교화 (Gram–Schmidt Orthogonalization) (2) | 2021.02.01 |
| [선형대수] 다중공선성 (Multicollinearity) 의 기하학적 의미 (0) | 2021.01.26 |
