[선형대수] 고유값과 고유벡터 (eigenvector & eigenvalue)
이름이 멋있는 eigenvector 와 eigenvalue 다른 개념과 같이 포스팅할까..? 하면서 미루다가 얼른 포스팅한다.
행렬대수학 수강당시에도 돌이켜보니..남은 것은 eigen vector 와 eigen value 뿐...이 랬던 것 같은데 다시 배우니 재밌다.
다음과 같은 순서로 포스팅 하겠다.
- Eigenvectors 와 Eigenvalues 의 개념
- 배우는 이유
- 어떻게 구하는지
1. Eigenvectors 와 Eigenvalues 의 개념
matrix 에 대한 중요한 정보를 가져오는 과정을 Eigen Decomposition 이라고 한다.
matrix A가 square matrix 로 주어질 때 (n x n), A의 eigenvector는 nonzero vector이고, 다음 식을 만족한다.
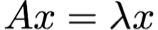
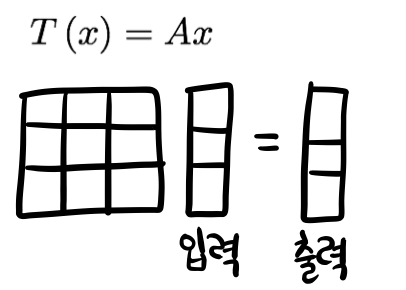
이 식은 linear transformation의 관점에서 본다면 A는 linear transformation이고, 입력벡터의 방향은 바꾸지 않고 크기만 바꾸는 변환이다.
i) 보통 일반적인 상황에서는, 입력벡터의 방향과 크기를 모두 바꾼다.

ii) T(x) = Ax = lambda x 는, 입력벡터의 방향은 바꾸지 않고 크기만 바꾼다.
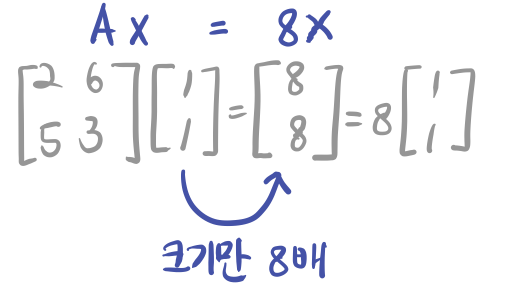
2. 왜 배우나? -> Computational Advantage 때문에 배운다.
Eigenvector와 Eigenvalue는 연산상의 장점을 가지고 있다. 행렬연산의 계산 횟수가 확연히 줄어드는데,
이는 GPU 병렬처리와 같이 다양한 문제의 key가 되는 행렬연산을 빨리 풀 수 있는 트릭을 발견한 것이다!
(머신러닝에서 이 행렬연산을 통한 병렬처리는 당연히 중요하다!)
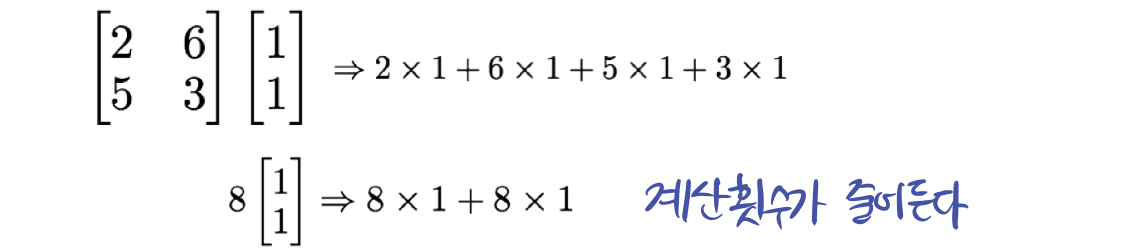
3. 어떻게 구하나?
결론적으로 간단히 수식적으로 풀면, 다음의 식을 풀면된다.
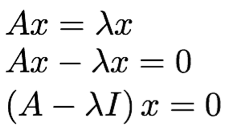
i) x (eigenvector) 가 0 vector 라면,
아까 eigenvector, x 는 nonzero vector 여야한다는 조건이 있었다.
0벡터는 방향성이 없고, 0을 대입하면 lambda 가 뭐든지 상관이 없어진다. 따라서 0벡터는 유의미하지 않기 때문에 고려하지 않는다.
ii) (A-lambda I) = 0 이라는 식은 새로운 linear system 이다.

이 식은 Ax = b 라고 볼 수 있다.
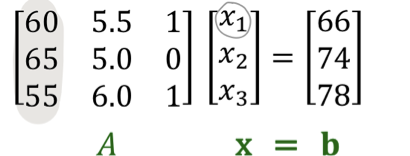
-
이 때 linearly dependent / independent 의 판단 : 저번에도 포스팅 했듯이, 벡터를 추가시킬 때 추가하는 column이 이전 column들의 span 에 들어가는지 여부로 판단한다. span에 안 들어갈 때 linearly independent 하다.
-
해의 존재 여부 : b가 A(재료벡터) 의 span에 들어간다면, 해가 존재한다.
iii) 결론적으로 (A-lambda I )x = 0 에서
A-lambda I 가 linearly dependent 한 column 을 가질 때, non-trivial solution x, eigenvector가 된다.
A가 linearly independent 할 때, Ax=0 을 만들면 x 에 대한 solution 은 0 벡터 밖에 없다.
A에다가 lambda 를 잘 빼서 linearly dependent한 column으로 바뀌어야한다. 따라서 det(A - lambda I) = 0 의 방정식을 풀게 되는 것이다.
이 lambda를 찾는 과정이 eigenvector와 eigenvalue를 구하는 과정이 된다.
det(A - lambda I) = 0 에 대한 자세한 내용은 Null Space & EigenSpace 개념과 함께 다음에 포스팅 하도록 하겠다.
Reference
주재걸 교수님의 인공지능을 위한 선형대수
'🤖 Today-I-Learned ] > Statistics & Machine Learning' 카테고리의 다른 글
| Hölder's inequality 증명 (0) | 2021.05.27 |
|---|---|
| [선형대수] Null Space 와 Orthogonal Complement (4) | 2021.02.21 |
| [선형대수] QR분해 (QR Factorization) (0) | 2021.02.02 |
| [선형대수] 그람-슈미트 직교화 (Gram–Schmidt Orthogonalization) (2) | 2021.02.01 |
| [선형대수] 다중공선성 (Multicollinearity) 의 기하학적 의미 (0) | 2021.01.26 |
[선형대수] 고유값과 고유벡터 (eigenvector & eigenvalue)
이름이 멋있는 eigenvector 와 eigenvalue 다른 개념과 같이 포스팅할까..? 하면서 미루다가 얼른 포스팅한다.
행렬대수학 수강당시에도 돌이켜보니..남은 것은 eigen vector 와 eigen value 뿐...이 랬던 것 같은데 다시 배우니 재밌다.
다음과 같은 순서로 포스팅 하겠다.
- Eigenvectors 와 Eigenvalues 의 개념
- 배우는 이유
- 어떻게 구하는지
1. Eigenvectors 와 Eigenvalues 의 개념
matrix 에 대한 중요한 정보를 가져오는 과정을 Eigen Decomposition 이라고 한다.
matrix A가 square matrix 로 주어질 때 (n x n), A의 eigenvector는 nonzero vector이고, 다음 식을 만족한다.
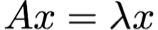

이 식은 linear transformation의 관점에서 본다면 A는 linear transformation이고, 입력벡터의 방향은 바꾸지 않고 크기만 바꾸는 변환이다.
i) 보통 일반적인 상황에서는, 입력벡터의 방향과 크기를 모두 바꾼다.

ii) T(x) = Ax = lambda x 는, 입력벡터의 방향은 바꾸지 않고 크기만 바꾼다.
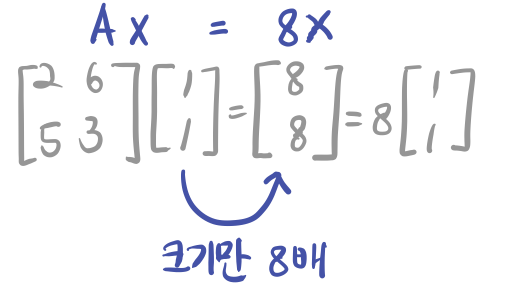
2. 왜 배우나? -> Computational Advantage 때문에 배운다.
Eigenvector와 Eigenvalue는 연산상의 장점을 가지고 있다. 행렬연산의 계산 횟수가 확연히 줄어드는데,
이는 GPU 병렬처리와 같이 다양한 문제의 key가 되는 행렬연산을 빨리 풀 수 있는 트릭을 발견한 것이다!
(머신러닝에서 이 행렬연산을 통한 병렬처리는 당연히 중요하다!)
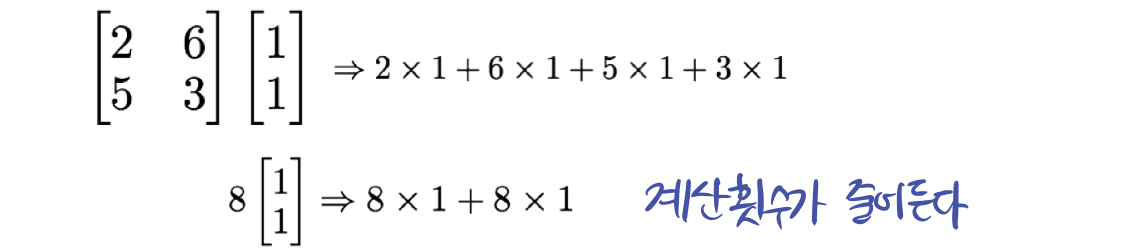
3. 어떻게 구하나?
결론적으로 간단히 수식적으로 풀면, 다음의 식을 풀면된다.
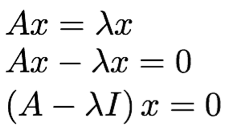
i) x (eigenvector) 가 0 vector 라면,
아까 eigenvector, x 는 nonzero vector 여야한다는 조건이 있었다.
0벡터는 방향성이 없고, 0을 대입하면 lambda 가 뭐든지 상관이 없어진다. 따라서 0벡터는 유의미하지 않기 때문에 고려하지 않는다.
ii) (A-lambda I) = 0 이라는 식은 새로운 linear system 이다.

이 식은 Ax = b 라고 볼 수 있다.
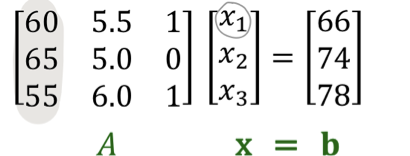
-
이 때 linearly dependent / independent 의 판단 : 저번에도 포스팅 했듯이, 벡터를 추가시킬 때 추가하는 column이 이전 column들의 span 에 들어가는지 여부로 판단한다. span에 안 들어갈 때 linearly independent 하다.
-
해의 존재 여부 : b가 A(재료벡터) 의 span에 들어간다면, 해가 존재한다.
iii) 결론적으로 (A-lambda I )x = 0 에서
A-lambda I 가 linearly dependent 한 column 을 가질 때, non-trivial solution x, eigenvector가 된다.
A가 linearly independent 할 때, Ax=0 을 만들면 x 에 대한 solution 은 0 벡터 밖에 없다.
A에다가 lambda 를 잘 빼서 linearly dependent한 column으로 바뀌어야한다. 따라서 det(A - lambda I) = 0 의 방정식을 풀게 되는 것이다.
이 lambda를 찾는 과정이 eigenvector와 eigenvalue를 구하는 과정이 된다.
det(A - lambda I) = 0 에 대한 자세한 내용은 Null Space & EigenSpace 개념과 함께 다음에 포스팅 하도록 하겠다.
Reference
주재걸 교수님의 인공지능을 위한 선형대수
'🤖 Today-I-Learned ] > Statistics & Machine Learning' 카테고리의 다른 글
| Hölder's inequality 증명 (0) | 2021.05.27 |
|---|---|
| [선형대수] Null Space 와 Orthogonal Complement (4) | 2021.02.21 |
| [선형대수] QR분해 (QR Factorization) (0) | 2021.02.02 |
| [선형대수] 그람-슈미트 직교화 (Gram–Schmidt Orthogonalization) (2) | 2021.02.01 |
| [선형대수] 다중공선성 (Multicollinearity) 의 기하학적 의미 (0) | 2021.01.26 |
